slam框架
1
2
3
4
5
6
| graph LR
A[传感器信息读取]-->B[前端视觉里程计]
B-->C["后端(非线性优化)"]
C-->D[建图]
A-->E[回环检测]
E-->C
|
三维空间刚体运动
旋转矩阵
点、向量、坐标系
任意向量在指定的基(e1,e2,e3)下有一坐标
a=[e1,e2,e3]⎣⎢⎡a1a2a3⎦⎥⎤=a1e1+a2e2+a3e3
(a1,a2,a3)T称为a在此基下的坐标。
对于a,b∈R3,内积为
a⋅b=aTb=i=1∑3aibi=∣a∣∣b∣cos⟨a,b⟩
外积
a×b=⎣⎢⎡e1a1b1e2a2b2e2a3b3⎦⎥⎤=⎣⎢⎡a2b3−a3b2a3b1−a1b3a1b2−a2b1⎦⎥⎤=⎣⎢⎡0a3−a2−a30a1a2−a10⎦⎥⎤b≜a∧b
a∧=⎣⎢⎡0a3−a2−a30a1a2−a10⎦⎥⎤
a∧是一个反对称函数。
坐标间的欧氏变换
某单位正交基(e1,e2,e3)经过旋转得到(e1′,e2′,e3′),对于一个向量a,在两个坐标系下的坐标为[a1,a2,a3]T和[a1′,a2′,a3′],那么有
[e1e2e3]⎣⎢⎡a1a2a3⎦⎥⎤=[e1′e2′e3′]⎣⎢⎡a1′a2′a3′⎦⎥⎤
对等式左右同时左乘⎣⎢⎡e1Te2Te3T⎦⎥⎤,得到
⎣⎢⎡a1a2a3⎦⎥⎤=⎣⎢⎡e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′⎦⎥⎤⎣⎢⎡a1′a2′a3′⎦⎥⎤≜Ra′
R称为旋转矩阵。
R是行列式为1的正交矩阵。
n维旋转矩阵构成特殊正交群SO(n):
SO(n)={R∈Rn×n∣RRT=I,det(R)=1}.
RT刻画了一个相反的旋转
a′=R−1a=RTa
把旋转和平移合到一起,得到
a′=Ra+t
变换矩阵与齐次坐标
重写上式,得到
[a′1]=[R0Tt1][a1]≜T[a1]
在三维坐标末尾添1,得到齐次坐标。称矩阵T为变换矩阵
依靠齐次坐标和变换矩阵,两次变换叠加可以写成
b~=T1a~,c~=T2b~⇒c~=T1T2a~
变换矩阵构成特殊欧氏群$$SE(n)$$:
SE(n)={T=[R0Tt1]∈R(n+1)×(n+1)∣R∈SO(3),t∈Rn×n}
T−1=[RT0T−RTt1]
旋转向量和欧拉角
旋转向量
任意旋转都可以用一个旋转轴n和一个旋转角θ来刻画。我们可以使用一个向量,其方向与旋转轴一致,长度对于旋转角,这种向量称为旋转向量(轴角/角轴)。
罗德里格斯公式
R=cosθI+(1−cosθ)nnT+sinθtr(n∧)
两边取迹,得到
tr(R)=cosθtr(I)+(1−cosθ)tr(nnT)+sinθtr(n∧)=3cosθ+(1−cosθ)=1+2cosθ
由此
θ=arccos2tr(R)−1
旋转轴上的向量在旋转后不发生改变:
Rn=n
由此,转轴n是矩阵R的特征值1对应的特征向量。求解此方程归一化后就可以得到旋转轴。
这样,我们就得到了旋转矩阵与旋转向量的转换关系。
欧拉角
欧拉角使用三个分离的转角,把一个旋转分解成3次绕不同轴的旋转。
常用的一种欧拉角是使用“偏航-俯仰-滚转”(yaw-pitch-roll)3个转角描述旋转,等价于ZYX轴的旋转。对任意旋转分解如下:
- 绕物体的Z轴旋转,得到偏航角yaw。
- 绕旋转之后的Y轴旋转,得到俯仰角pitch。
- 绕旋转之后的X轴旋转,得到滚转角roll。
此时,任意旋转可以使用[r,p,y]T三维向量描述。
欧拉角的重大缺点是会遇到万向锁问题:在俯仰角为±90∘时,第一次旋转与第三次旋转共用一个轴使得系统丢失一个自由度。这称为奇异性问题。
四元数
四元数是紧凑的,没有奇异性。
q=q0+q1i+q2j+q3k
i,j,k是四元数的三个虚部。
⎩⎪⎪⎪⎨⎪⎪⎪⎧i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−j
有时,也用一个标量和一个向量表示四元数:
q=[s,v]T,s=q0∈R,v=[q1,q2,q3]T∈R3
s称为四元数实部,而v称为它的虚部,如果虚部为0,称为实四元数;反之,实部为0,称为虚四元数。
四元数运算
有两个四元数qa=[sa,va]T,qb=[sb,vb]T
-
加法和减法
qa±qb=[sa±sb,va±vb]T
-
乘法
qaqb=[sasb−vaTvb,savb+sbva+va×vb]T
四元数乘法通常是不可交换的,除非va,vb共线。
-
模长
∣qa∣=sa2+vaTva
∣qaqb∣=∣qa∣∣qb∣
-
共轭
qa∗=[sa,−va]T
q∗q=qq∗=[s2+vTv,0]T=[∣qa∣2,0]T
-
逆
q−1=∣q∣2q∗
qq−1=q−1q=1
(qaqb)−1=qa−1qb−1
-
数乘
kq=[ks,kv]T
四元数表示旋转
空间中一三维点p=[x,y,z]∈R3,以及单位四元数q指定的旋转。p经过旋转之后变为p′。使用矩阵表述,有p′=Rp。
使用四元数,如下
p=[0,x,y,z]T=[0,v]T
相当于把四元数的3个虚部与空间中三个轴对应。那么,旋转后的p′可表示为:
p′=qpq−1
四元数到其他旋转表示的变换
设q=[s,v]T,定义如下记号
q+=[sv−vTsI+v∧],q⊕=[sv−vTsI−v∧]
于是,可以把四元数乘法写成矩阵形式
q1+q2=[sv1−v1TsI+v1∧][s2v2]=[s1s2−v1Tv2s1v2+s2v1+v1∧v2]=q1q2
同理,有
q1q2=q1+q2=q2⊕q1
根据前面说法,有
p′=qpq−1=q+p+q−1=q+(q−1)⊕p
q+(q−1)⊕=[sv−vTsI+v∧][s−vvTsI+v∧]=[10T0vvT+s2I+2sv∧+(v∧)2]
由此,
R=vvT+s2I+2sv∧+(v∧)2
对上式求迹,得到
tr(R)=tr(vvT)+3s2+2s⋅0+tr((v∧)2)=v12+v22+v32+3s2−2(v12+v22+v32)=(1−s2)+3s2−2(1−s2)=4s2−1
θ=arccos2tr(R)−1=arccos(2s2−1)
cosθ=2s2−1=2cos22θ−1⇒θ=2arccoss
四元数到旋转向量的转换公式为
⎩⎪⎨⎪⎧θ=2arccosq0[nx,ny,nz]T=sin2θ[q1,q2,q3]T
其中,
sin2θ=q12+q22+q32
相似、仿射、射影变换
-
相似变换
允许对物体进行均匀缩放
TS=[sR0Tt1]
三维相似变换的集合称为相似变换群,记作Sim(3)。
-
仿射变换
TA=[A0Tt1]
只要求A是可逆矩阵。仿射变换后,保证每个平行四边形面是平行四边形。
-
射影变换
最一般的变换
TP=[AaTtv]
保证平面相交相切不变。
李群、李代数
李群李代数基础
群
群是一种集合加上一种运算的代数结构。把集合记作A,运算记作·,那么群可以记作G=(A,⋅)。群要求运算满足以下条件:
- 封闭性:∀a1,a2∈A,a1⋅a2∈A
- 结合律:∀a1,a2,a3∈A,(a1⋅a2)⋅a3=a1⋅(a2⋅a3)
- 幺元:∃a0∈A,s.t.∀a∈A,a0⋅a=a⋅a0=a
- 逆:∀a∈A,∃a−1∈A,s.t.a⋅a−1=a0
李群是指具有连续(光滑)性质的群。
李代数引出
RRT=I⇒R(t)R(t)T=I⇒R˙(t)R(t)T+R(t)R˙(t)T=0⇒R˙(t)R(t)T=−(R˙(t)R(t)T)T
可见,R˙(t)R(t)T是一个反对称矩阵。
若
a∧=A
记
A∨=a
对于R˙(t)R(t)T,我们可以找到一个ϕ(t)∈R3与之对应
R˙(t)R(t)T=ϕ(t)∧
右乘R(t),得到
R˙(t)=ϕ(t)∧R(t)
可见,每对R(t)求一次导,只需要左乘一个ϕ(t)∧,考虑t0=0时,设此时R(0)=I。把R(t)在t=0附近泰勒展开:
R(t)≈R(t0)+R˙(t0)(t−t0)=I+ϕ(t0)∧I(t−0)=I+ϕ(t0)∧(t)
由于ϕ反映了R的导数性质,故称它在SO(3)原点附近的正切空间上。同时在t0附近,设ϕ保持常数ϕ(t0)=ϕ0,那么有
R˙(t)=ϕ(t0)∧R(t)=ϕ0∧R(t)
这是一个关于R的微分方程,有初始值R(0)=I,解得
R(t)=eϕ0∧t
旋转矩阵R与另一个反对称矩阵ϕ0∧t通过指数关系发生了联系。
给定某个时刻的R,就能求得一个ϕ,它描述了R在局部的导数关系。ϕ正对应到SO(3)上的李代数so(3)。
李代数的定义
每个李群都有对应的李代数李代数描述了李群的局部性质,是单位元附近的正切空间。一般李代数定义如下:
李代数由集合V、数域F和二元运算符[ ,]组成。如果满足以下性质,则(V,F,[,])构成一个李代数记作g:
-
封闭性 ∀X,Y∈V,[X,Y]∈V
-
双线性 ∀X,Y,Z∈V,a,b∈F,有
[aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[Z,X]+b[Z,Y]
-
自反性 ∀X∈V,[X,X]=0
-
雅可比恒等式
∀X,Y,Z∈V,[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0
二元运算称为李括号,李括号表达了两个元素的差异。
李代数so(3)
之前提到的ϕ事实上是一种李代数。SO(3)对应的李代数是定义在R3上的向量,记作ϕ。每个ϕ都可以生成一个反对称矩阵:
Φ=ϕ∧=⎣⎢⎡0ϕ3−ϕ2−ϕ30ϕ1ϕ2−ϕ10⎦⎥⎤∈R3×3
两个向量ϕ1,ϕ2对应的李括号为
[ϕ1,ϕ2]=(Φ1Φ2−Φ2Φ1)∨
不引起歧义的情况下,so(3)的元素是三维向量或三维反对称矩阵,不加区别:
so(3)={ϕ∈R3,Φ=ϕ∧∈R3×3}
李代数se(3)
SE(3)对应的李代数是定义在R6上的向量:
se(3)={ξ=[ρϕ]∈R6,ρ∈R3,ϕ∈so(3),ξ∧=[ϕ∧0Tρ0]∈R4×4}
李括号:
[ξ1,ξ2]=(ξ1∧ξ2∧−ξ2∧ξ1∧)∨
指数与对数映射
对so(3)中的任意元素ϕ,定义指数映射:
exp(ϕ∧)=n=0∑∞n!1(ϕ∧)n
将ϕ记作ϕ=∣ϕ∣ϕ^,对于ϕ^∧有:
ϕ^∧ϕ^∧=⎣⎢⎡−(ϕ^2)2−(ϕ^3)2ϕ^1ϕ^2ϕ^1ϕ^3ϕ^1ϕ^2−(ϕ^1)2−(ϕ^3)2ϕ^2ϕ^3ϕ^1ϕ^3ϕ^2ϕ^3−(ϕ^1)2−(ϕ^2)2⎦⎥⎤=ϕ^ϕ^T−I
以及
ϕ^∧ϕ^∧ϕ^∧=ϕ^∧(ϕ^ϕ^T−I)=−ϕ^∧
这样
exp(ϕ∧)=exp(∣ϕ∣ϕ^∧)=n=0∑∞n!1(∣ϕ∣ϕ^∧)n=I+∣ϕ∣ϕ^∧+2!1(∣ϕ∣ϕ^∧)2+3!1(∣ϕ∣ϕ^∧)3+4!1(∣ϕ∣ϕ^∧)4+…=ϕ^ϕ^T−ϕ^∧ϕ^∧+∣ϕ∣ϕ^∧+2!1∣ϕ∣2ϕ^∧ϕ^∧−3!1∣ϕ∣3ϕ^∧−4!1∣ϕ∣4ϕ^∧ϕ^∧+…=ϕ^ϕ^T+(∣ϕ∣−3!1∣ϕ∣3+5!1∣ϕ∣5−…)ϕ^∧−(1−2!1∣ϕ∣2+4!1∣ϕ∣4−…)ϕ^∧ϕ^∧=ϕ^∧ϕ^∧+I+sin∣ϕ∣ϕ^∧−cos∣ϕ∣ϕ^∧ϕ^∧=(1−cos∣ϕ∣)ϕ^∧ϕ^∧+I+sin∣ϕ∣ϕ^∧=cos∣ϕ∣I+(1−cos∣ϕ∣)ϕ^ϕ^T+sin∣ϕ∣ϕ^∧
注意到,这就是罗德里格斯公式。
R=cosθI+(1−cosθ)aaT+sinθa∧
由此,so(3)实际上就是旋转向量组成的空间,指数映射对应罗德里格斯公式。反之,定义对数映射:
ϕ=ln(R)∨=(n=0∑∞n+1(−1)n(R−I)n+1)∨
可以用求角轴的方法求。
对于se(3),这里直接给出公式
exp(ξ∧)=⎣⎢⎡∑n=0∞n!1(ϕ∧)n0T∑n=0∞(n+1)!1(ϕ∧)nρ1⎦⎥⎤≜[R0TJρ1]=TJ=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧
李代数求导与扰动模型
BCH公式与近似公式
BCH公式(Baker-Campbell-Hausdorff)完整形式见https://en.wikipedia.org/wiki/Baker%E2%80%93Campbell%E2%80%93Hausdorff_formula
这里只给出前几项:
ln(exp(A)exp(B))=A+B+21[A,B]+121[A,[A,B]]−121[B,[A,B]]+…
SO(3)下的BCH近似为:
ln(R1R2)∨=ln(exp(ϕ1∧)exp(ϕ2∧))∨≈{Jl(ϕ2)−1ϕ1+ϕ2当ϕ1为小量Jr(ϕ1)−1ϕ2+ϕ1当ϕ2为小量Jl=J=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧Jl−1=2θcot2θI+(1−2θcot2θ)aaT−2θa∧Jr(ϕ)=Jl(−ϕ)
ΔR⋅R=exp(Δϕ∧)exp(ϕ∧)=exp((ϕ+Jl−1(ϕ)Δϕ)∧)exp((ϕ+Δϕ)∧)=exp((JlΔϕ)∧)exp(ϕ∧)=exp(ϕ∧)exp((JrΔϕ)∧)ΔT⋅T=exp(Δξ∧)exp(ξ∧)=exp((ξ+Jl−1(ξ)Δξ)∧)T⋅ΔT=exp(ξ∧)exp(Δξ∧)=exp((ξ+Jr−1(ξ)Δξ)∧)
李代数求导
将一个空间点p旋转得到Rp。计算旋转之后点坐标相对于旋转的导,非正式记为
∂R∂Rp
省略转置运算,上式就是计算
∂ϕ∂(exp(ϕ∧)p)=δϕ→0limδϕexp((ϕ+δϕ)∧)p−exp(ϕ∧)p=δϕ→0limδϕexp((Jlδϕ)∧)exp(ϕ∧)p−exp(ϕ∧)p=δϕ→0limδϕ(I+(Jlδϕ)∧)exp(ϕ∧)p−exp(ϕ∧)p=δϕ→0limδϕ(Jlδϕ)∧exp(ϕ∧)p=δϕ→0limδϕ−(exp(ϕ∧)p)∧Jlδϕ=−(Rp∧)Jl
由此,
∂R∂Rp=−(Rp∧)Jl
扰动模型(左乘)
另一种求导方式是对R进行一次扰动ΔR,看结果相对于扰动的变化率。这个扰动可以乘在左边也可以乘在右边,最后结果会有一点儿微小的差异,以左扰动为例。设左扰动ΔR对应的李代数为φ。然后,对φ求导,即
∂φ∂(Rp)=φ→0limφexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p=φ→0limφ(I+φ∧)exp(ϕ∧)p−exp(ϕ∧)p=φ→0limφφ∧Rp=φ→0limφ−(Rp)∧φ=−(Rp)∧
SE(3)上的扰动模型
将一个空间点p变换得到Tp。给T左乘扰动ΔT=exp(δξ∧),设扰动项李代数为δξ=[δρ,δϕ]T,那么:
∂δξ∂(Tp)=[I0T−(Rp+t∧)0T]≜(Tp)⊙
评估轨迹误差
估计轨迹Testi,i,真实轨迹Tgt,i,其中i=1,2,…,N
绝对轨迹误差(ATE)
ATEall=N1i=1∑N∣ln(Tgt,i−1Testi,i)∨∣2
绝对平移误差
ATEtans=N1i=1∑N∣trans(Tgt,i−1Testi,i)∣2
trans表示只取平移部分
相对位姿误差(RPE)
考虑i到i+Δt时刻的运动
RPEall=N−Δt1i=1∑N−Δt∣ln((Tgt,i−1Tgt,i+Δt)−1(Testi,i−1Testi,i+Δt))∨∣2
相对平移误差
RPEtrans=N−Δt1i=1∑N−Δt∣trans((Tgt,i−1Tgt,i+Δt)−1(Testi,i−1Testi,i+Δt))∨∣2
相似变换群和李代数
相似变换
p′=[sR0Tt1]=sRp+t
相似变换群
Sim(3)={S=[sR0Tt1]∈R4×4}
李代数
sim(3)={ζ∣ζ=⎣⎢⎡ρϕσ⎦⎥⎤∈R7,ζ∧=[σI+ϕ∧0Tρ0]∈R4×4}
指数映射
exp(ζ∧)=[eσexp(ϕ∧)0TJsρ1]Js=σeσ−1I+σ2+θ2σeσsinθ+(1−eσcosθ)θa∧+(σeσ−1+σ2+θ2(eσcosθ−1)σ+(eσsinθ)θ)a∧a∧
扰动模型
∂ζ∂Sp=[I0T−q∧0Tq0]
相机与图像
相机模型
针孔相机模型
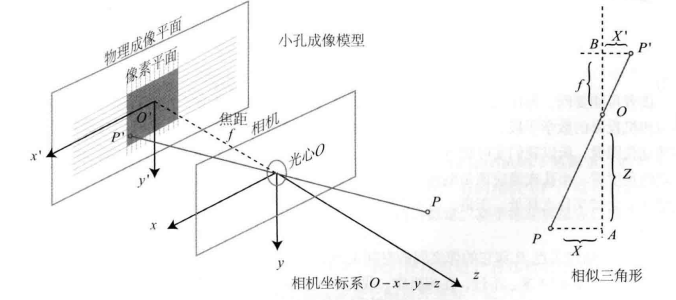
P[X,Y,Z]T→P′[X′,Y′,Z′]T,设小孔焦距f,得到
fZ=−X′X=−Y′Y
去掉负号,得到
fZ=X′X=Y′Y⇒⎩⎪⎪⎨⎪⎪⎧X′=fZXY′=fZY
传感器将感受到的光线转换成图像像素。在成像平面上固定一个像素平面o−u−v,得到P′的像素坐标[u,v]T。u轴向右,v轴向下。设像素坐标在u轴上缩放α倍,在v轴上缩放β倍,原点平移[cx,cy]T,得到:
{u=αX′+cxv=βY′+cy⇒⎩⎪⎪⎨⎪⎪⎧u=fxZX′+cxv=fyZY′+cy
Z⎣⎢⎡uv1⎦⎥⎤=⎣⎢⎡fx000fy0cxcy1⎦⎥⎤⎣⎢⎡XYZ⎦⎥⎤≜KP
K称为相机内参数矩阵,确定相机内参称为标定。
P点的世界坐标Pw,位姿由旋转矩阵R和平移向量t描述。
ZPuv=Z⎣⎢⎡uv1⎦⎥⎤=K(RPw+t)=KTPw
R,t称为相机外参数。
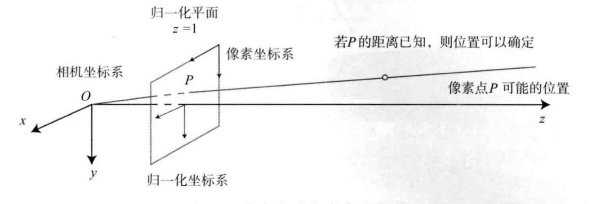
归一化:
(RPw+t)=[X,Y,Z]T→[ZX,ZY,1]T
点的深度在投影过程中丢失了。
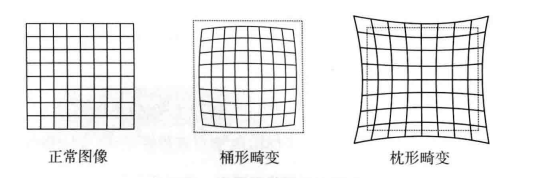
畸变
由透镜引起的畸变称为径向畸变,分为桶形畸变和枕形畸变。
相机组装过程中不能使透镜和成像面严格平行,引入切向畸变。
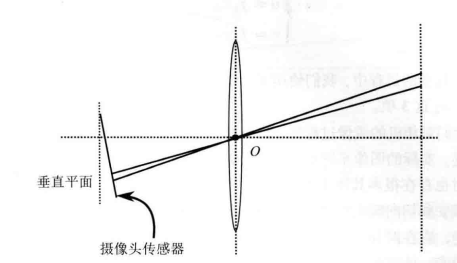
对于相机坐标系中的一点P,我们能够通过5个畸变系数找到这个点在像素平面上的正确位置:
-
将三维空间点投影到归一化图像平面。设它的归一化坐标为[x,y]T
-
对归一化平面上的点计算径向畸变和切向畸变。
{xdistorted=x(1+k1r2+k2r4+k3r6)+2p1xy+p2(r2+2x2)ydistorted=y(1+k1r2+k2r4+k3r6)+2p2xy+p1(r2+2y2)
-
将畸变后的点通过内参数矩阵投影到像素平面,得到该点在图像上的正确位置。
{u=fxxdistorted+cxv=fyydistorted+cy
单目相机的成像过程:
- 世界坐标系下有一个固定的点P,世界坐标为Pw。
- 由于相机在运动,它的运动由R,t或变换矩阵T∈SE(3)描述。P的相机坐标为P~c=RPw+t。
- 这时的P~c的分量为X,Y,Z,把它们投影到归一化平面Z=1上,得到P的归一化坐标:Pc=[X/Z,Y/Z,1]T。
- 有畸变时,根据畸变参数计算Pc。发生畸变后的坐标。
- P的归一化坐标经过内参后,对应到它的像素坐标:Puv=KPc。
双目相机模型
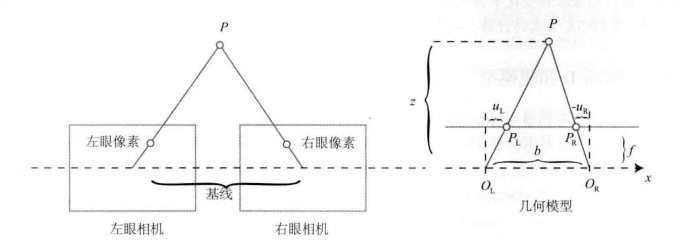
zz−f=fracb−uL+uRb⇒z=dfb,d≜uL−uR
b——基线,d——视差
RGB-D相机模型
红外结构光
飞行时间






